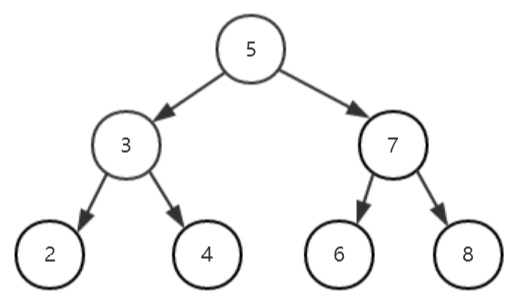
一、平衡二叉树是带有平衡条件的二叉查找树
平衡条件:平衡二叉树的每个结点的左子树和右子树的高度最多差1。
平衡因子 bf :左子树的高度减去右子树的高度,显然 bf 的取值范围是 [ -1, 1 ] 。每一个结点(在其结点结构中)保留平衡因子 bf 。
/* 平衡二叉树的结点结构 */ struct BinaryTreeNode { int bf; // 平衡因子,当前结点的左右子树的高度差 int value; BinaryTreeNode *lChild; BinaryTreeNode *rChild;}; 补:虽然平衡二叉树能确保树的高度为O(logn),但同时我们对其的插入/删除操作都需保持它的平衡条件。
由于平衡二叉树的平衡条件比较严格,故其维护的代价也较大,一般只适用于查找次数多、插入和删除次数少的情况。
从实际出发,平衡条件较为宽松的红黑树是更好的选择,因为对其进行插入或删除操作付出的代价相对较小。
当然,如果在应用场景中插入和删除操作并不频繁,只是对查找要求较高,那么平衡二叉树还是较优于红黑树。
二、旋转操作——保持平衡二叉树的平衡条件
1. 失衡的四种情况(把当前因失衡而必须重新平衡的结点叫做α)
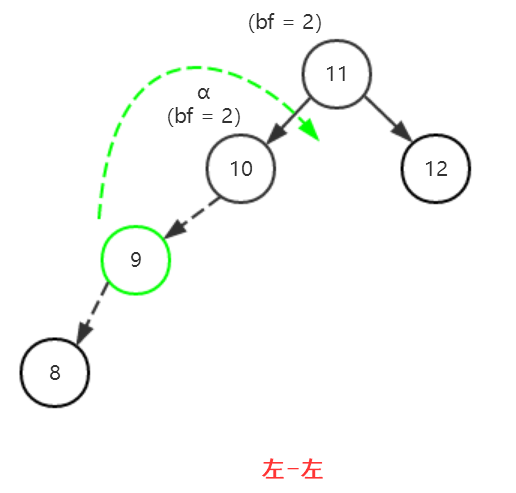
- 对α的左儿子的左子树进行一次插入(左-左情况,以α为轴右旋)
- 对α的左儿子的右子树进行一次插入(左-右情况,先左旋,再右旋)
- 对α的右儿子的左子树进行一次插入(右-左情况,先右旋,再左旋)
- 对α的右儿子的右子树进行一次插入(右-右情况,以α为轴左旋)




绿色的结点为新加入的结点。虚线连接的三个结点是涉及旋转的结点。虚线的方向代表相应的失衡情况。
2. 示例
【左-右】(涉及的双旋结点为8、9、10)
(1)以8为轴进行左旋(逆时针旋转)

(2)以10为轴进行右旋(顺时针旋转)
(3)得到平衡二叉树

分析:当有多个结点的 | bf | > 1时,需要重新平衡的结点 α 是离新加入结点最近的。
【右-左】(涉及的双旋结点为7、15、16)
(1)以16为轴进行右旋(顺时针旋转)

(2)以7为轴进行左旋(逆时针旋转)

(3)得到平衡二叉树
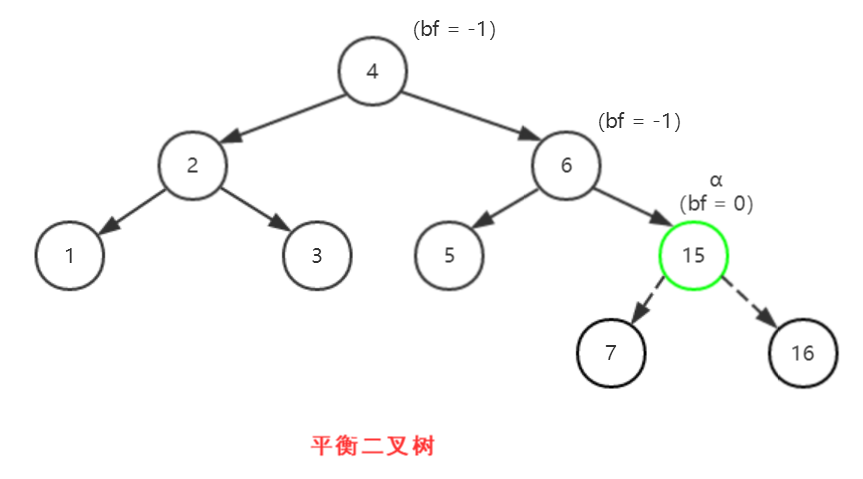
【右-左】涉及的双旋结点为6、7、15
(1)以15为轴进行右旋(顺时针旋转)
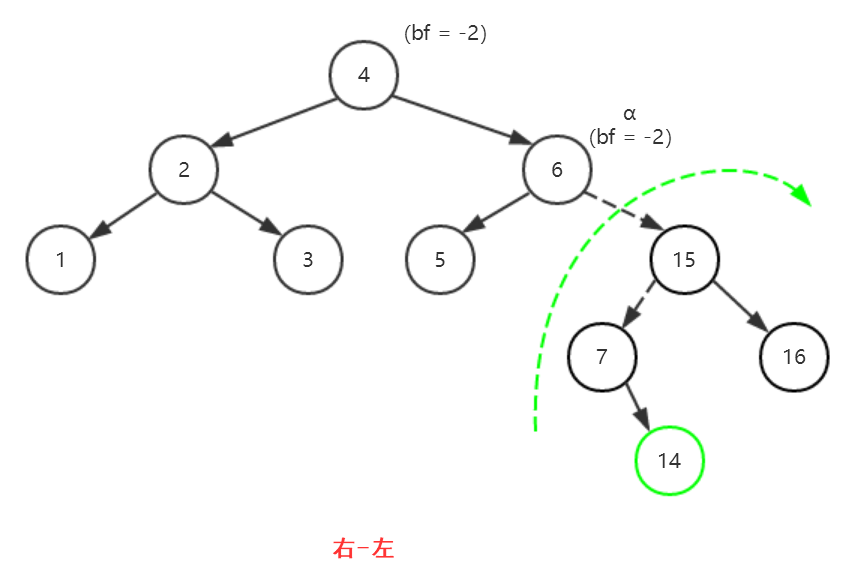
(2)以6为轴进行左旋(逆时针旋转)
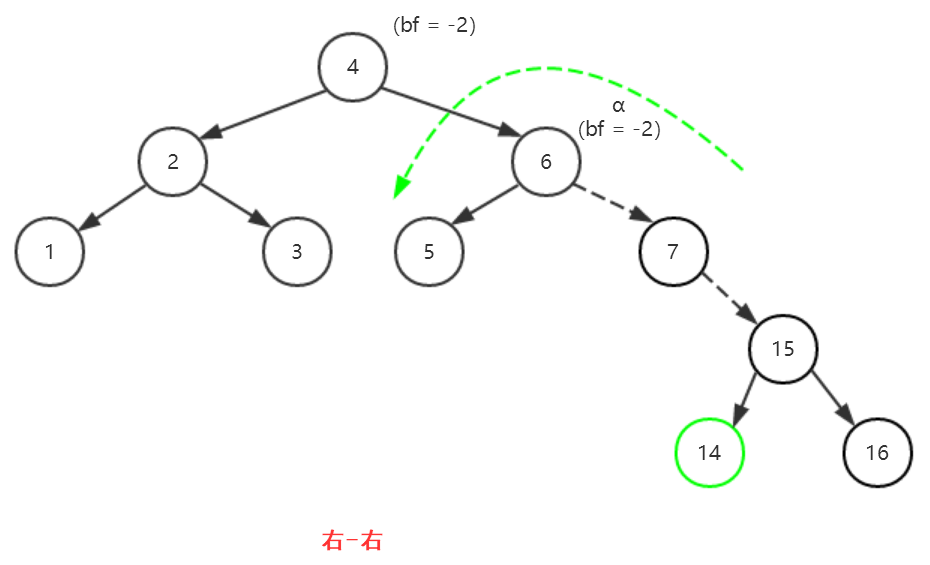
(3)得到平衡二叉树
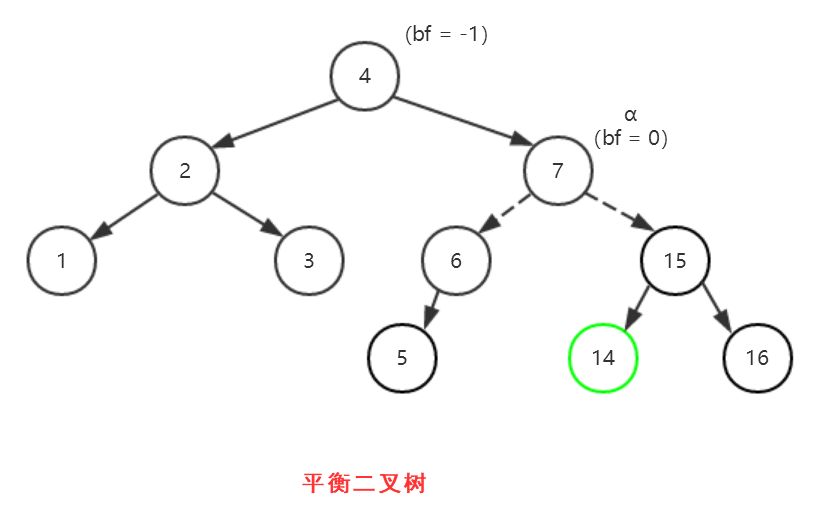
【小结:如何判断是哪种失衡情况】
结点α:离新加入结点最近的且| bf | > 1 的结点 。

以上图为例,结点α为6,然后再观察从结点α到新加入的结点14形成的路径“6-->15-->7-->14”,发现“6-->15-->7”形成的正是右-左这一情况。
3. 代码
// 左旋:借助图来写代码 void LRotate(BinaryTreeNode **pRoot){ BinaryTreeNode *pNewRoot = (*pRoot)->rChild; // 新的根结点是当前根结点的右子树 (*pRoot)->rChild = pNewRoot->lChild; // 新的根结点的左子树应挂载到根结点的右子树 pNewRoot->lChild = *pRoot; // 新的根结点的左子树是当前根结点 *pRoot = pNewRoot; // 修改当前根结点的指向 } // 右旋:借助图来写代码void RRotate(BinaryTreNode **pRoot){ BinaryTreeNode *pNewRoot = (*pRoot)->lChild; (*pRoot)->lChild = pNewRoot->rChild; pNewRoot->rChild = *pRoot; *pRoot = pNewRoot;} /* 左平衡:pRoot的左子树高于右子树,需平衡左子树 *//* 先检查失衡情况是左-左还是左-右 * 左-左情况:(*pRoot)->lChild->bf的值为1(即LH) * 左-右情况:(*pRoot)->lChild->bf的值为-1(即RH) */ void LeftBalance(BinaryTreeNode **pRoot){ BinaryTreeNode *lChild, *lChild_rChild; // 左孩子,左孩子的右孩子 lChild = (*pRoot)->lChild; lChild_rChild = lChild->rChild; switch(lChild->bf) { // 左-左情况 case LH: lChild->bf = (*pRoot)->bf = EH; // 作用和RH情况下的switch语句 RRotate(pRoot); // 以pRoot为轴左旋 break; // 左-右情况 case RH: // 该switch语句的作用是更新各个结点的bf值,它们对应调整后的值 switch(lChild_rChild->bf) { case LH: (*pRoot)->bf = RH; lChild->bf = EH; break; case RH: (*pRoot)->bf = EH; lChild->pf = LH; break; case EH: (*pRoot)->bf = EH; lChild->pf = EH; default: break; } lChild_rChild->bf = EH; // 调整后的新的根结点为lChild_rChild LRotate(&lChild); // 以lChild为轴左旋 RRotate(pRoot); // 以pRoot为轴右旋 break; }} /* 右平衡:pRoot的右子树高于左子树,需平衡右子树 *//* 先检查失衡情况是右-右还是右-左 * 右-右情况:(*pRoot)->rChild->bf的值为-1(即RH) * 右-左情况:(*pRoot)->rChild->bf的值为1(即lH) */ void RightBalance(BinaryTreeNode **pRoot) { BinaryTreeNode *rChild, *rChild_lChild; // 右孩子,右孩子的左孩子 rChild = (*pRoot)->rChild; rChild_lChild = rChild->lChild; switch(rChild->bf) { case RH: rChild->bf = (*pRoot)->bf = EH; LRotate(pRoot); break; case LH: switch(rChild_lChild->bf) { case LH: (*pRoot)->bf = EH; rChild->bf = RH; break; case RH: (*pRoot)->bf = LH; rChild->bf = EH; break; case EH: (*pRoot)->bf = EH; rChild->bf = EH; break; default: break; } rChild_lChild->bf = EH; RRotate(&rChild); LRotate(pRoot); break; }}
三、插入操作
/* 往平衡二叉树上插入结点 */bool insert(BinaryTreeNode **pRoot, int x, bool *isTaller){ // 找到插入位置(树中没有值等于x的结点) if(*pRoot == nullptr) { *pRoot = new BinaryTreeNode; (*pRoot)->bf = EH; (*pRoot)->value = x; (*pRoot)->lChild = nullptr; (*pRoot)->rChild = nullptr; *isTaller = true; return true; } else { // 树中有值为x的结点,不用插入了 if((*pRoot)->value == x) { *taller = false; return false; } // 往左子树中插入 if((*pRoot->value) > x) { // 树中有相同的结点,直接返回 if(!insert(&((*pRoot)->lChild), x, isTaller)) { *isTaller = false; return false; } // isTaller为真,则意味着树长高了,并且往左子树中插入了结点 if(*isTaller) { // 检查平衡因子bf,根据相应的情况做出对应的修改和旋转 switch((*pRoot)->bf) { // LH表示在插入该结点之前,左子树就比右子树高1 // 故插入该结点后,左子树将比右子树高2 case LH: LeftBalance(pRoot); // 使左子树平衡 *isTaller = false; // 已平衡,令isTaller为假,往上递归就不再进入此语句了 break; // 在插入该结点之前,右子树比左子树高1 case RH: (*pRoot)->bf = EH; *isTaller = false; break; // 在插入该结点之前,左子树和右子树一样高 // 故插入该结点后,左子树将比右子树高1 case EH: (*pRoot)->bf = LH; *isTaller = true; // 继续往上递归 break; } } } // 往右子树中插入 else { if(!insert(&((*pRoot)->rChild), x, isTaller)) { *isTaller = false; return false; } // isTaller为真,则意味着往右子树中插入了结点 if(*isTaller) { switch((*pRoot)->bf) { case LH: (*pRoot)->bf = EH; *isTaller = false; break; case RH: RightBalance(pRoot); *isTaller = false; break; case EH: (*pRoot)->bf = RH; *isTaller = true; break; } } } } }
四、完整代码
#include#include #include using namespace std;#define EH 0 // 等高 #define LH 1 // 左高 #define RH -1 // 右高 /* 二叉平衡树的结点结构 */ struct BinaryTreeNode { int bf; // 平衡因子,当前结点的左右子树的高度差 int value; BinaryTreeNode *lChild; BinaryTreeNode *rChild;}; // 左旋:借助图来写代码 void LRotate(BinaryTreeNode **pRoot){ BinaryTreeNode *pNewRoot = (*pRoot)->rChild; // 新的根结点是当前根结点的右子树 (*pRoot)->rChild = pNewRoot->lChild; // 新的根结点的左子树应挂载到根结点的右子树 pNewRoot->lChild = *pRoot; // 新的根结点的左子树是当前根结点 *pRoot = pNewRoot; // 修改当前根结点的指向 } // 右旋:借助图来写代码void RRotate(BinaryTreeNode **pRoot){ BinaryTreeNode *pNewRoot = (*pRoot)->lChild; (*pRoot)->lChild = pNewRoot->rChild; pNewRoot->rChild = *pRoot; *pRoot = pNewRoot;} /* 左平衡:pRoot的左子树高于右子树,需平衡左子树 *//* 先检查失衡情况是左-左还是左-右 * 左-左情况:(*pRoot)->lChild->bf的值为1(即LH) * 左-右情况:(*pRoot)->lChild->bf的值为-1(即RH) */ void LeftBalance(BinaryTreeNode **pRoot){ BinaryTreeNode *lChild, *lChild_rChild; // 左孩子,左孩子的右孩子 lChild = (*pRoot)->lChild; lChild_rChild = lChild->rChild; switch(lChild->bf) { // 左-左情况 case LH: lChild->bf = (*pRoot)->bf = EH; // 作用和RH情况下的switch语句 RRotate(pRoot); // 以pRoot为轴左旋 break; // 左-右情况 case RH: // 该switch语句的作用是更新各个结点的bf值,它们对应调整后的值 switch(lChild_rChild->bf) { case LH: (*pRoot)->bf = RH; lChild->bf = EH; break; case RH: (*pRoot)->bf = EH; lChild->bf = LH; break; case EH: (*pRoot)->bf = EH; lChild->bf = EH; default: break; } lChild_rChild->bf = EH; // 调整后的新的根结点为lChild_rChild LRotate(&lChild); // 以lChild为轴左旋 RRotate(pRoot); // 以pRoot为轴右旋 break; }} /* 右平衡:pRoot的右子树高于左子树,需平衡右子树 *//* 先检查失衡情况是右-右还是右-左 * 右-右情况:(*pRoot)->rChild->bf的值为-1(即RH) * 右-左情况:(*pRoot)->rChild->bf的值为1(即lH) */ void RightBalance(BinaryTreeNode **pRoot) { BinaryTreeNode *rChild, *rChild_lChild; // 右孩子,右孩子的左孩子 rChild = (*pRoot)->rChild; rChild_lChild = rChild->lChild; switch(rChild->bf) { case RH: rChild->bf = (*pRoot)->bf = EH; LRotate(pRoot); break; case LH: switch(rChild_lChild->bf) { case LH: (*pRoot)->bf = EH; rChild->bf = RH; break; case RH: (*pRoot)->bf = LH; rChild->bf = EH; break; case EH: (*pRoot)->bf = EH; rChild->bf = EH; break; default: break; } rChild_lChild->bf = EH; RRotate(&rChild); LRotate(pRoot); break; }}/* 往平衡二叉树上插入结点 */bool insert(BinaryTreeNode **pRoot, int x, bool *isTaller){ // 找到插入位置(树中没有值等于x的结点) if(*pRoot == nullptr) { *pRoot = new BinaryTreeNode; (*pRoot)->bf = EH; (*pRoot)->value = x; (*pRoot)->lChild = nullptr; (*pRoot)->rChild = nullptr; *isTaller = true; return true; } else { // 树中有值为x的结点,不用插入了 if((*pRoot)->value == x) { *isTaller = false; return false; } // 往左子树中插入 if((*pRoot)->value > x) { // 树中有相同的结点,直接返回 if(!insert(&((*pRoot)->lChild), x, isTaller)) { *isTaller = false; return false; } // isTaller为真,则意味着树长高了,并且往左子树中插入了结点 if(*isTaller) { // 检查平衡因子bf,根据相应的情况做出对应的修改和旋转 switch((*pRoot)->bf) { // LH表示在插入该结点之前,左子树就比右子树高1 // 故插入该结点后,左子树将比右子树高2 case LH: LeftBalance(pRoot); // 使左子树平衡 *isTaller = false; // 已平衡,令isTaller为假,往上递归就不再进入此语句了 break; // 在插入该结点之前,右子树比左子树高1 case RH: (*pRoot)->bf = EH; *isTaller = false; break; // 在插入该结点之前,左子树和右子树一样高 // 故插入该结点后,左子树将比右子树高1 case EH: (*pRoot)->bf = LH; *isTaller = true; // 继续往上递归 break; } } } // 往右子树中插入 else { if(!insert(&((*pRoot)->rChild), x, isTaller)) { *isTaller = false; return false; } // isTaller为真,则意味着往右子树中插入了结点 if(*isTaller) { switch((*pRoot)->bf) { case LH: (*pRoot)->bf = EH; *isTaller = false; break; case RH: RightBalance(pRoot); *isTaller = false; break; case EH: (*pRoot)->bf = RH; *isTaller = true; break; } } } } }/* 中序遍历 */ void InOrderTraverse(BinaryTreeNode *pRoot){ if(pRoot == nullptr) return; InOrderTraverse(pRoot->lChild); cout << pRoot->value; InOrderTraverse(pRoot->rChild);}/* 求树的高度 */int GetHeight(BinaryTreeNode *pRoot){ if(pRoot == nullptr) return 0; int leftHeight = GetHeight(pRoot->lChild); int rightHeight = GetHeight(pRoot->rChild); return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;} int main(){ int arr[7] = {4, 3, 2, 7, 6, 8, 5}; BinaryTreeNode *pTree = nullptr; bool isTaller = false; for (int i = 0; i < 7; ++i) { insert(&pTree, arr[i], &isTaller); } cout << "提示:平衡二叉树创建完毕!" << endl; cout << "提示:树的高度为" << GetHeight(pTree) << endl; cout << "提示:中序遍历平衡二叉树!" << endl; InOrderTraverse(pTree); cout << endl; return 0;}
测试结果:

上段代码建立的平衡二叉树的最理想高度应为3,但由于平衡二叉树的平衡条件是允许左右子树存在高度差的,故代码运行结果为4。下图为理想情况下应建立的二叉树。